Randomness in Balatro
How the RNG works.
Randomness is almost everywhere in electronic games — when picking up a new card or weapon, choosing the boss at the next level, and even generating the world. In rogue-like games like Balatro, randomness is rather important as it brings some uncertainness to your game experience. Randomness in Balatro is pseudo, and so is in most rogue-like games. Given a global seed and a specified game state, the next “random” number is almost predictable, given that you know the PRNG algorithm under the hood. This is a clever design that allows players to reproduce their game experience and share it with each other.
The more time I spent on playing Balatro, the deeper my fascination grows with its essence of randomness. Simple questions accumulated:
- How does
 Judgement choose the Joker card to create?
Judgement choose the Joker card to create? - Which joker card does
 Invisible Joker choose to duplicate?
Invisible Joker choose to duplicate? - What’s the likelihood of acquiring
 The Soul in the Spectral and Arcana packs?
The Soul in the Spectral and Arcana packs?
Most of the time I’ll utilize SL (save & load) to avoid bad results, for example the Invisible Joker duplicates a useless Joker card. However, it’s helpful if you know one or two principles about these randomnesses. As a result, you can control the game somehow, relative to the three examples:
- “Store” a Joker card in Judgement.
- Control the Joker card to duplicate.
- Understand why you seldom see legendary Joker cards 😄.
In this blog I’ll try to analyze and explain how randomness works in Balatro. All code in this blog is based on Balatro 1.0.1o-FULL.
Core Randomness Functions
Balatro provides several utility functions for randomness. Let’s first check pseudoseed:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function pseudoseed(key, predict_seed)
if key == 'seed' then return math.random() end
if predict_seed then
local _pseed = pseudohash(key..(predict_seed or ''))
_pseed = math.abs(tonumber(string.format("%.13f", (2.134453429141+_pseed*1.72431234)%1)))
return (_pseed + (pseudohash(predict_seed) or 0))/2
end
if not G.GAME.pseudorandom[key] then
G.GAME.pseudorandom[key] = pseudohash(key..(G.GAME.pseudorandom.seed or ''))
end
G.GAME.pseudorandom[key] = math.abs(tonumber(string.format("%.13f", (2.134453429141+G.GAME.pseudorandom[key]*1.72431234)%1)))
return (G.GAME.pseudorandom[key] + (G.GAME.pseudorandom.hashed_seed or 0))/2
end
We can ignore the first two if blocks at this moment, because they are just corner cases that are rarely triggered. This function can a sequence of generate random seeds for each individual key, for example "lucky_mult". The current random seed is forwarded using the LCG algorithm, i.e. $X_{n+1} = (a X_{n}+c)\ \mathrm{mod}\ m$, where $a = 1.72431234$, $c=2.134453429141$ and $m=1$.
Given the global seed G.GAME.pseudorandom.seed in this game, we can “predict” the sequence of random seeds for each key, since the algorithm is deterministic. Seeds are used to produce random numbers:
1
2
3
4
5
6
function pseudorandom(seed, min, max)
if type(seed) == 'string' then seed = pseudoseed(seed) end
math.randomseed(seed)
if min and max then return math.random(min, max)
else return math.random() end
end
Try to Predict the Randomness!
What’s the first joker card in the first buffoon pack? First a number that indicates the rarity is generated with the key 'rarity1buf'. Then the pool of all available joker cards is constructed, and the index of the chosen joker is generated with the key 'Joker'..rarity..'buf1'. To see more details, read the definition of create_card in functions/common_events.lua. I write a simple Lua script to emulate this process.
1
2
$ lua balatro_get_first_joker.lua DFRU5D52
The first joker in the first buffoon pack (at ante 1) is [Blueprint].
You may not reproduce the same result. Even worse, you may accidentally find
pseudorandomalways returns two numbers, totally losing its randomness. The reason is that LÖVE, the game engine behind Balatro, applies LuaJIT as its compiler. Compared with the standard Lua implementation which uses the platform-specified ANSIrand(), LuaJIT uses a Tausworthe PRNG with period $2^{223}$ to implementmath.random()andmath.randomseed()(see more details in LuaJIT extensions). To get the same result, you should install LuaJIT, or simply employ LÖVE.
Oh, the first joker card of seed DFRU5D52 is our beloved  Blueprint! Let’s check it. All kinds of decks and all levels of stakes are applicable.
Blueprint! Let’s check it. All kinds of decks and all levels of stakes are applicable.
Case Study
Judgement
The Tarot card Judgement creates a random joker card by the create_card routine:
1
local card = create_card('Joker', G.jokers, self.ability.name == 'The Soul', nil, nil, nil, nil, self.ability.name == 'Judgement' and 'jud' or 'sou')
It’s similar to create the joker cards for buffoon packs, but the keys for PRNG are independent. In this process, two sequences of random numbers are used:
- the rarity of the generated joker
- the index of the generated joker in the available pool
Two keys for pseudoseed are required. If we can change these keys, the “random” result will change too. Also, the pool of available joker cards affects the result. In conclusiton, the following actions may change which joker card Judgement creates:
- Increase/decrease the ante (the two keys changes).
- Buy/sell a joker (the pool changes).
- Reroll the shop (the pool changes).
For example, if you find Judgement creates a useless joker card, you can save/load, keep Judgement in your consumable slots, and create a card again after you defeat the boss blind and get into the next ante.
Invisible Joker
When you sell an Invisible Joker, your owned joker cards are collected, and then a random joker card is chosen:
1
local chosen_joker = pseudorandom_element(jokers, pseudoseed('invisible'))
Here the key is determined, so we can only control the jokers table to change the result. Balatro orders your owned jokers by the time you obtain them. For example, if you obtain the joker cards A, B, C, D sequentially in this game, the variable jokers is {A, B, C, D}. If the Invisible Joker duplicate C, you know that the current index is 3, which cannot be changed unless you sell another Invisible Joker (then the pseudorandom seed is forwarded). If you do want to duplicate D, just sell one of A, B or C. But there is no way to duplicate A or B, in this case.
The Soul
When a Tarot card or Spectral card is created, a random number is generated to decide whether The Soul comes in and replaces it:
1
2
3
if pseudorandom('soul_'.._type..G.GAME.round_resets.ante) > 0.997 then
forced_key = 'c_soul'
end
At each ante, the key remains the same. But the possibility is extremely small — only when the random number is bigger than 0.997, i.e. 0.3%! We cannot control this probability at all. Open arcana packs and spectral packs as more as possible, and just pray!
The Lucky Money
 Lucky cards have the probability of 1 in 15 to give you 20 dollars when scored. The key of its pseudurandom seeds is identical:
Lucky cards have the probability of 1 in 15 to give you 20 dollars when scored. The key of its pseudurandom seeds is identical:
1
2
3
4
if pseudorandom('lucky_money') < G.GAME.probabilities.normal/15 then
self.lucky_trigger = true
ret = ret + self.ability.p_dollars
end
The only way to earn more money from lucky cards is playing them as more as possible! If the scored lucky card does not give you anything, it’s not necessary to save/load and cancel this hand, or you’ll still get nothing next time. Just play them and go through more pseudorandom seeds.
Discussion: The Toxic Seeds
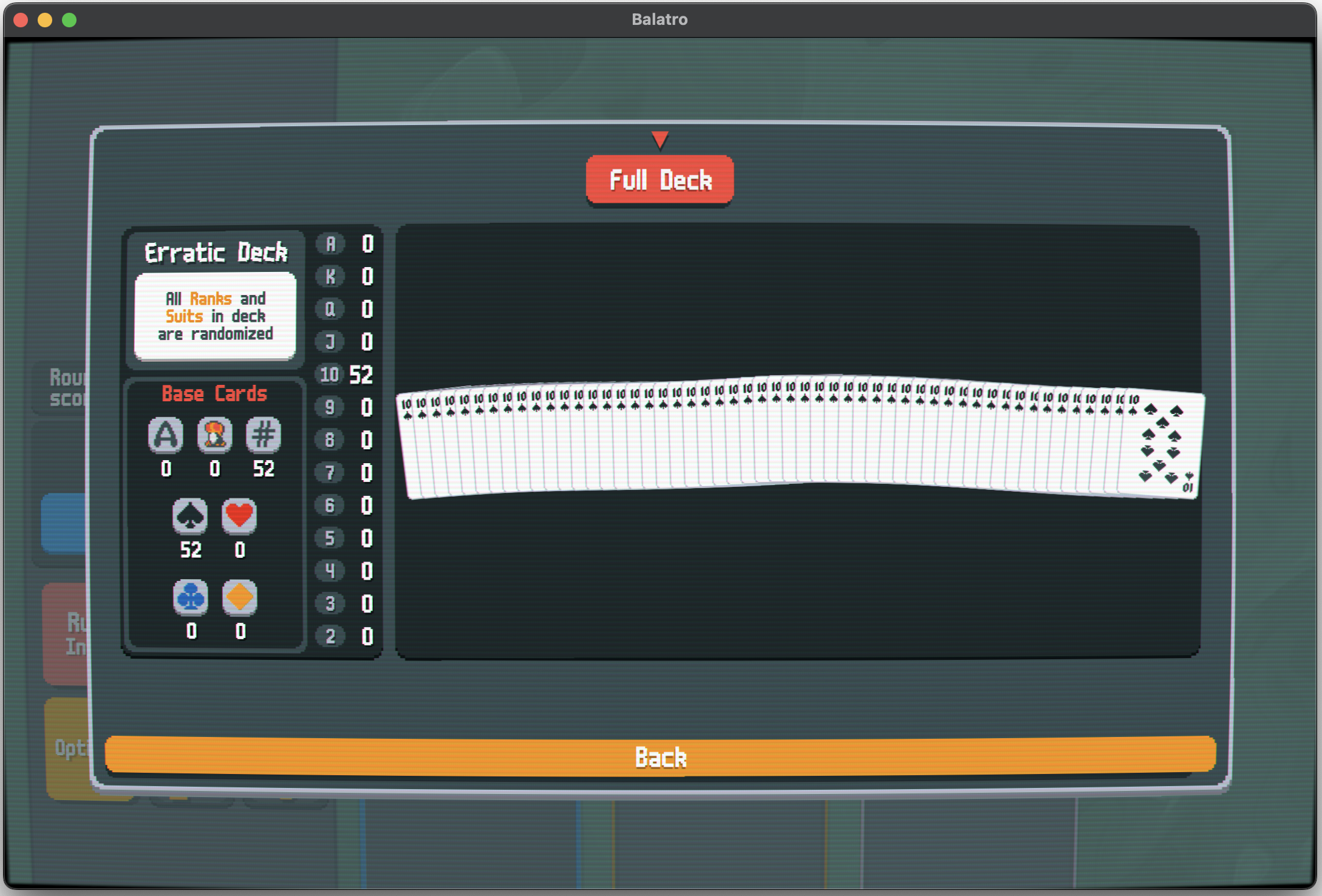
The  Erratic Deck is erratic: Try the seed
Erratic Deck is erratic: Try the seed XEQH7CP9 with any stake, you will get an incomprehensible deck:
What, 52 spade tens?! Well, this possibility is intuitively tiny, but in fact it’s almost impossible in the probability theory!
First let’s consider how many decks the erratic deck may generate. Assume we have 52 non-negative integer $a_i$ ($i = 1,2,\cdots,52$), and each variable indicates the number of a specified card in our deck. Then, given the deck size is 52, we have:
\[\sum_{i=1}^{52}{a_i} = 52.\]Our problem transforms into determining the number of solutions to this diophantine equation. This is factually a combination problem, and the answer is
\[N_1 = C_{51}^{103} = \frac{103!}{51!\cdot 52!}=791532924062974587678774064068\approx 7.92\times 10^{29}.\]However, the number of overall seeds in Balatro is
\[N_2 = (26+9)^{8} = 2251875390625 \approx 2.25 \times 10^{12}.\]A seed in Balatro consists of 8 uppercase letters and Arabic numerals. However, Balatro treats
0(the numeral zero) andO(the letter afterNand beforePin alphabet) identically.
In other words, if the likelihood of each deck appearing is equally probable, then the probability that a deck generated by some seed(s) consists of 52 identical cards is
\[p = 1 - \left(\frac{N1-52}{N_1}\right)^{N_2} \approx 1.48 \times 10^{-16}.\]If you have little intuitive grasp of just how minuscule this probability truly is, let me show you some statistics:
- The probability that a man is struck by lightning is 1 in 1,000,000 per year.
- The probability that you play a royal flush in Holdem is $1.54\times 10^{-6}$.
- The probability that an asteroid crashes on Earth within the next second is about $10^{-15}$.
When the probability of an event is so small, we can just consider it as “impossible”. Not to mention that not only XEQH7CP9 generates this deck (try RV35TK35 too). So how can such a coincidence happen in Balatro?
The problem comes from the pseudohash function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function pseudohash(str)
if true then
local num = 1
for i=#str, 1, -1 do
num = ((1.1239285023/num)*string.byte(str, i)*math.pi + math.pi*i)%1
end
return num
else
str = string.sub(string.format("%-16s",str), 1, 24)
local h = 0
for i=#str, 1, -1 do
h = bit.bxor(h, bit.lshift(h, 7) + bit.rshift(h, 3) + string.byte(str, i))
end
return tonumber(string.format("%.13f",math.sqrt(math.abs(h))%1))
end
end
This function hashes str to a number. It travels the string from end to beginning, update the number with the formula at line 5. Note that num is never greater than 1 because it’s taken the modulus by 1 each time. You may notice the problem: will num become less and less, and suddenly turns to zero because of insufficient precision of float? The answer is, yes. When hashing the string erraticXEQH7CP9, the process how num changes is
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
0.38664478504086
0.55995656190294
0.32349394214634
0.022266708739835
0.89992220806744
0.226694001059
1.6370904631913e-11
0
nan
nan
nan
nan
nan
nan
nan means Not-A-Number in Lua. Any mathematical operation on nan results in nan. Therefore, the final pseudorandom seed is always nan, and if you give nan as the seed for math.randomseed, math.random can only generate one number.
1
2
math.randomseed(1/0)
print(math.random()) -- => 0.98541213607668
Spade ten is always chosen when this number is used to pick a game card. Therefore, these toxic seeds always creates a deck consists of 52 spade tens.
If you dig deeper, you’ll find there are more seeds leading to some “impossible” events, like all appeared joker cards are holographic, every scored lucky card gives 20 dollars…… Well, most of the time we are unaware of the intrinsic glitch behind the pseudorandom algorithm, but that’s not a big deal. After all, we can still play the game happily. Someone who is bored may spend time investigating it, and come up with some interesting but useless conclusions. ☺️